
Air Force Research Lab
Summer Faculty Fellowship Program

Cislunar Integrator Analysis and Maneuver Detection
Sponsoring Research Lab and Location: Air Force Maui Optical Supercomputing (AMOS) site, Maui, HI
AFRL Advisor: Capt. Zachary Funke
Faculty Advisor: Dr. Aaron J. Rosengren
Abstract
Accurate state estimation is imperative for extending space domain awareness (SDA) to the xGEO (beyond geosynchronous orbit) regime, a key objective of the 15th Space Surveillance Squadron (SPSS). Numerical integrators, tools that predict the positions and velocities of satellites given the governing force models, are an essential component of state estimation and have been thoroughly validated at GEO and below. But, families of orbits beyond these altitudes, such as Earth-Moon Lyapunov orbits, accumulate large state errors quickly when utilizing legacy integrators. Moreover, these families of orbits are frequently becoming the operational destination for artificial satellites as NASA, along with other private entities, prepares to launch Gateway, the first space station in lunar orbit. In this report, we conduct an analysis of state-of-the-art, open-source numerical integrators, comparing their respective accuracies in predicting the states of an object in a near-rectilinear halo orbit (NRHO). Additionally, we develop an extensible framework for retrospectively detecting orbit maneuvers in the xGEO regime.
1 Statement of Objectives
I. Integrator-Error Analysis and Model-Fidelity Comparison. Numerical integrators for astrodynamical systems, both legacy and state-of-the-art, have primarily been utilized for propagating artificial satellites dominated by weakly perturbed Keplerian dynamics [1–3]. Contrarily, satellites transferring between the spheres of influence of multiple celestial bodies are governed by dynamics that can not be represented as perturbations of Keplerian motion; and as such, legacy integrators
that are based on this fundamental assumption, like SGP4, lose accuracy rather quickly in these regimes [4, 5]. State-of-the-art integrators, such as GMAT [6], Goddard Space Flight Center’s mission analysis tool, and ASSIST [7], an open-source, ephemeris-quality extension of the n-body integrator REBOUND, are more adept at state propagation for cislunar objects than their traditional counterparts.
One of the current objectives of the 15th Space Surveillance Squadron (15SPSS), is optical detection of CAPSTONE [8], a 12U Cubesat in a near-rectilinear halo orbit (NRHO) about the L2 Earth-Moon libration point. Due to its extreme distance from the Earth, as well as its size, optical reconstruction of CAPSTONE requires a post-processing, pixel-stacking procedure that superimposes multiple images of the satellite to increase the magnitude of the signal. As these concurrent
images are taken at different epochs, stacking them requires accurate knowledge of CAPSTONE’s ephemeris, so as to match the direction of shifting the stacked images with the direction of travel. In cases where the ephemeris is not known, we plan to use precise numerical integrators to provide an accurate approximation of the true ephemeris, such that optical reconstruction is still possible. To ensure that numerical integrators can act as accurate approximations for the true ephemeris, we compare the propagated states of GMAT and ASSIST to the “true” ephemerides generated by JPL Horizons Web Service. Using the position and velocity residuals as the metric of accuracy, we determine the range of expected error/day of maneuver-free (i.e., ballistic) motion of CAPSTONE, and conclude how the fidelity of the present force model impacts that accuracy. Through this analysis, we look to confirm that ASSIST is a viable model for cislunar propagation, as the open-source software uses a numerical scheme called IAS15, a 15th-order integrator whose regularization procedure makes it equipped to handle close approaches without adaptive time-stepping, making it the faster option compared to GMAT. In addition, we perform a model-fidelity test that compares the accuracy of modeling CAPSTONE as both a restricted three-body and a restricted four-body problem. This final exercise is meant to measure the efficacy of using certain approximate models in the cislunar regime, specifically for objects in operational libration-point orbits (LPOs) in the Earth-Moon system.
II. Maneuver Detection of CAPSTONE via Cartesian State-Vector Inspection. The numerical integrators discussed thus far only function as accurate approximations of the true ephemeris during non-maneuvering (i.e., ballistic) periods. Therefore, the ability to detect that a maneuver has occurred is a necessity for performing the aforementioned integrator analysis. Maneuvers reveal themselves in the numerically integrated trajectory data as abrupt, non-differentiable shifts in Cartesian velocity error. By initializing simulations at states throughout the lifetime of CAPSTONE, and propagating these simulations through the maneuver points, we use a forensic inspection method to estimate whether, and when, a maneuver has occurred. We assume simulations initialized prior to this suspected changepoint are invalid approximations of the true ephemeris beyond said changepoint. Having confirmed a set of suspected maneuver points throughout the lifetime of CAPSTONE, we define maneuver-free windows where our integrator-accuracy analysis can be performed.
Furthermore, it is suspected that CAPSTONE’s swift passage through perilune would falsely trigger maneuvers, as this region is where the Cartesian states are changing the fastest. However, this region is also where the state uncertainty is greatest, as indicated by information provided by Advance Space, the owner and operator of CAPSTONE. They have informed us that maneuvers will likely not take place more frequently that once a week and will not occur near perilune. The exact window of allowable maneuver times was not provided, but using the information given, we develop ”no-go” zones near perilune, where perceived maneuver triggers are ruled out. The exact metric for this zone, as well as the change in velocity-error tolerance for triggering, will be discussed in Section 2.
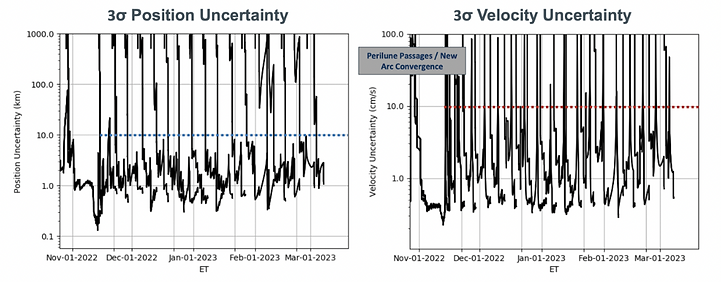
Figure 1: 3σ position and velocity uncertainties throughout the lifetime of CAPSTONE. Note that the periodic spikes in uncertainty occur near perilune.
2 Research Effort
2.1 Comparison of Residuals of Numerical Integrators
Technical Approach. Comparing the accuracy of numerical integrators and determining likely maneuver epochs are tasks that are coupled by nature. To accurately compare integrators to ephemerides, a maneuver-free period is required, thus maneuver detection is necessary. However, to confidently predict when maneuvers occur, an accurate numerical integrator is required, thus integrator analysis is necessary. To circumvent this paradox, we pick an epoch where the likelihood of CAPSTONE performing a maneuver is low (for instance, directly after insertion into the NRHO), and begin with a short period of integrator error analysis and comparison. Assuming no jarring errors indicate a rogue maneuver, we continue forward with maneuver detection, and confirm that the initial propagation window is unlikely to contain a maneuver.
Following the aforementioned procedure, we begin analysis of GMAT and ASSIST at Nov 15, 2022, 00:00:00 TDB, approximately one day after supposed insertion into the NRHO. We then propagate the initial conditions of CAPSTONE, provided by JPL Horizons, for 24 hours using both GMAT and ASSIST, and compare the propagated Cartesian positions and velocities to the ephemeris at corresponding epochs. Once we have confirmed that the initial propagation window contains no expected maneuvers via our maneuver detection procedure, we confirm a large maneuver-free propagation window, Nov 19, 2022, 00:00:00 to Dec 21, 2022, 00:00:00 TDB, perform an analysis over said window, and determine the expected state error growth/day of the respective GMAT and ASSIST models. We note that, based on discussions with Advanced Space on their planned orbital-maintenance maneuver (OMM) cadence, that this window is likely too large; yet, our initial assessments and heuristic maneuver-detection method did not identify any OMMs during this month-long period.
GMAT allows the flexibility to choose the perturbations present in the force model, while that contained within ASSIST’s is immutable. We perform analysis on multiple GMAT force models of varying fidelity to demonstrate the importance of including various “perturbative” forces. The same analysis is performed on the standard ASSIST force model, which includes the direct Newtonian attraction from the Sun, planets, Moon, Pluto, and 16 massive asteroids, the Sun’s J2 zonal
harmonic, the Earth’s J2, J3, and J4 zonal harmonics, and relativistic corrections. Note that both propagators allow for the inclusion of solar radiation pressure, which was omitted in this study.
Preliminary Results. Our initial analysis indicates that no maneuver took place in the 24-hour window from Nov 15, 2022, 00:00:00 to Nov 16, 2022, 00:00:00 TDB. Therefore, this propagation window serves as the timeline for both the preliminary integrator-error analysis test, which will determine and compare the accuracy of GMAT and ASSIST after a single, maneuver-free day, and the model-fidelity test, which compares the accuracy of approximate models for the cislunar regime.
In Figure 2, we compare four integrators to the Horizons ephemeris: ASSIST, GMAT-4BP, GMAT-EJ2, and GMAT-EMJ2. The ASSIST force model has been previously stated. GMAT-4BP includes the direct Newtonian attractions of the Earth, Sun, and Moon. GMAT-EJ2 adds a 50×50 gravity-field model of the Earth geopotential to GMAT-4BP. GMAT-EMJ2 adds a 50×50 gravity-field model of the Moon to GMAT-EJ2. We include the right-hand side sub-figures in Figure 2, which display the final hour of propagation to zoom in the focus and allow for visual inspection of the performance of the integrators. Additionally, Table 1 shows the final position and velocity error of each of the integrators, from which we can see the GMAT-4BP model is (paradoxically) the most accurate over this window. ASSIST’s GMAT counterpart is best considered to be GMAT-EJ2, as both include the J2 of the Earth, as well as point masses of all the other major planets in the Solar System, while also excluding the J2 of the Moon (ASSIST does include the J2 of the Sun, but the perturbation is insignificant at the current distance from the Sun, over the current time window). In this case, ASSIST’s final state error is only 0.8 m and 0.59 cm/s larger than GMAT-EJ2 final state error.
While we would expect the higher-fidelity models to be more accurate, we are unaware of the exact force model used by Advanced Space in their orbit-determination solution, and therefore cannot make further claims about these results before analyzing larger propagation windows

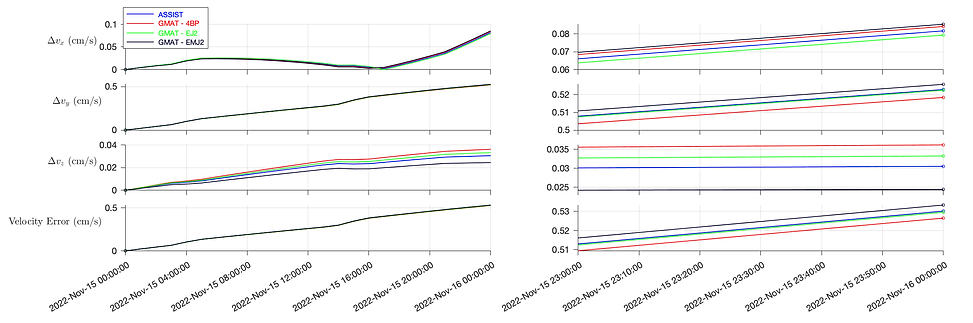
Figure 2: Cartesian state error of numerical integrators compared with the JPL Horizons ephemeris of CAPSTONE, from Nov 15, 2022 00:00:00 to Nov 16, 2022 00:00:00 TDB. The right sub-figures are zoomed-in versions of the left sub-figures. (top) ∆x, ∆y, ∆z, and position error (km). (bottom) ∆vx, ∆vy, ∆vz , and velocity error (cm/s).
To provide assurance that the initial propagation window is maneuver-free, we have included Figure 3, which displays the abruptness with which the velocity error jumps during what is suspected to be an OMM.
Table 1: Final state error at Nov 16, 2022, 00:00:00 TDB

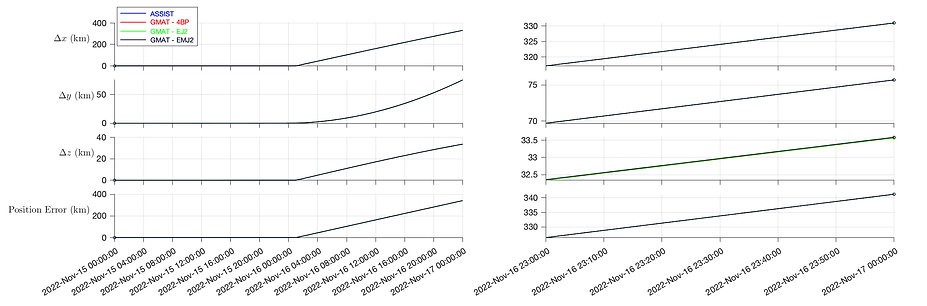
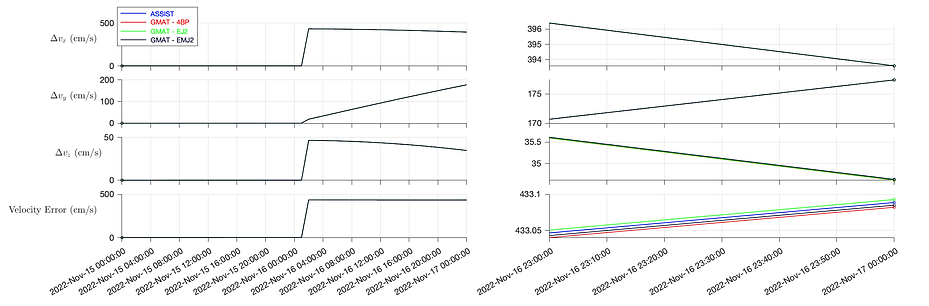
Figure 3: Cartesian state error over a propagation window containing a maneuver. The suspected the maneuver occurs a little after Nov 16, 2022, 00:00:00 TDB. The right sub-figures are zoomed-in versions of the left sub-figures. (top) ∆x, ∆y, ∆z, and position error (km). (bottom) ∆vx, ∆vy, ∆vz , and velocity error (cm/s).
Now, we perform the model-fidelity test: using GMAT, we compare the accuracy of modeling CAPSTONE with the restricted three-body (R3BP) and the restricted four-body problem (R4BP). The R3BP consists of the Earth, Moon, and CAPSTONE, while the R4BP model includes all of those as well as the Sun. All bodies are treated as point masses in both models. From Figure 4, we see that the R3BP model’s final error is greater than 50 km in position and 100 cm/s in velocity
after only a day of propagation, whereas the R4BP model is far more accurate, as can be seen in Table 1. This exercise emphasizes the importance of including the Sun in any approximate models meant for performing accurate state estimation in the cislunar regime. By extension, we conclude that the phenomenological CR3BP and the ER3BP, models of lower fidelity than the R3BP, are unfit for state estimation of objects in LPOs.

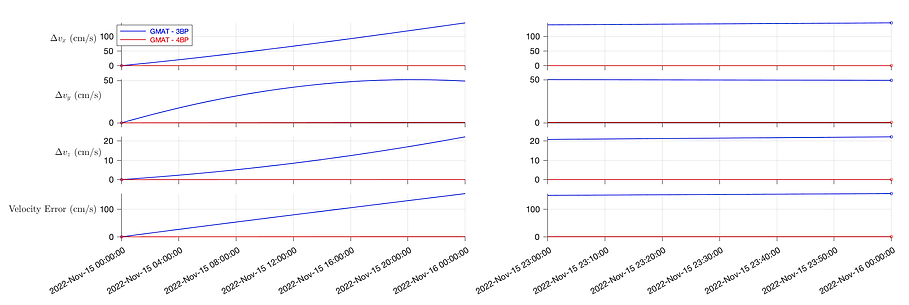
Figure 4: Cartesian state error of the R3BP and R4BP from Nov 15, 2022 00:00:00 to Nov 16, 2022 00:00:00 TDB.
Using the maneuver-detection procedure discussed in Section 2.2, we confirm a longer maneuver-free propagation window, from Nov 19, 2022 00:00:00 to Dec 21, 2022, 00:00:00 TDB. Those results, displayed in Figures 5 and 6, demonstrate the error behavior over this 32 day propagation period. At times of perilune passage, we see large spikes in error in both position and velocity; for velocity, that error recedes after passage is concluded, but for position, we see a secular growth in error with each passage. In addition, we note that over this longer propagation window, ASSIST
and GMAT-EJ2 are more accurate vs the R4BP modeled by GMAT-4BP. This is the expected result, however, what is unexpected is that the highest fidelity model, GMAT-EMJ2, is the least accurate. We can most likely conclude from this that Advanced Space does not include the Moon’s J2 zonal harmonic in their orbit-determination solution. Figure 6 removes this model to give more focus to the error comparison of the more accurate models. Those final errors, as well as the expected state error growth over this 32 day period, can be found in Table 2.
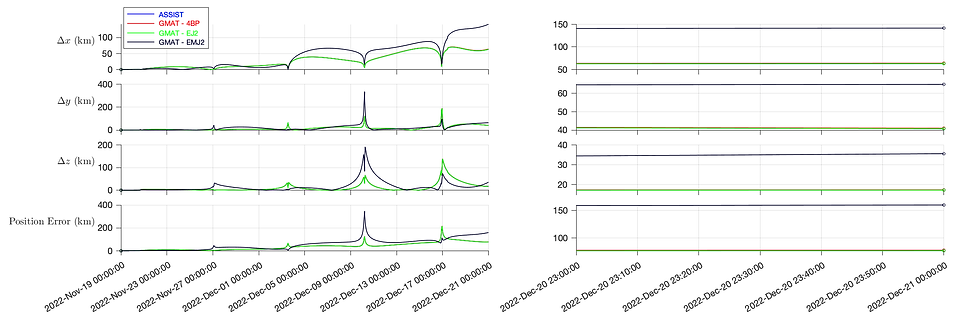
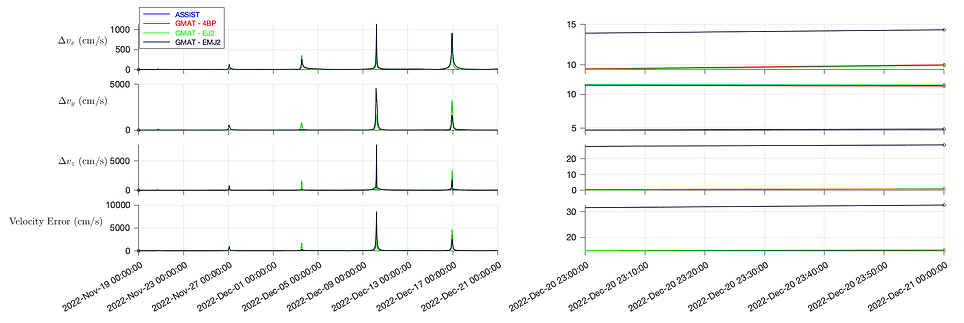
Figure 5: Cartesian state error of numerical integrators compared with the JPL Horizons ephemeris of CAPSTONE, from Nov 19, 2022 00:00:00 to Dec 21, 2022 00:00:00 TDB.


Figure 6: Cartesian state error of numerical integrators compared with the JPL Horizons ephemeris of CAPSTONE, from Nov 19, 2022 00:00:00 to Dec 21, 2022 00:00:00 TDB, excluding GMAT-EMJ2 to clarify the final state errors.
Table 2: Final state error and state-error growth from Nov 19, 2022, 00:00:00 to Dec 21, 2022, 00:00:00 TDB

2.2 Maneuver Detection via Cartesian-State Inspection
Technical Approach. Maneuvers often go unreported in public ephemeris repositories; thus, detecting their existence to confirm the accuracy of the numerical integrators is necessary. We suspect that large, instantaneous shifts in the velocity error between observation epochs are representative of maneuvers. As a preliminary assessment, we perform a forensic inspection of the Cartesian state residuals, specifically the velocity error of ASSIST and the ephemeris, over time. We also make the assumption that maneuvers will not be performed near perilune, where uncertainties are the highest, which we have initially taken to mean 90% of the lunar Hill region (LHR), the radius rLHR of which is defined as

where aM is the semi-major axis of the Moon, and mM and mE are the masses of the Moon and Earth, respectively. Excluding jumps in velocity error of a certain tolerance in these zones, we return retrospective estimates of times where we believe CAPSTONE maneuvers occurred. The tolerance we have chosen is 5 cm/s, as we were informed by Advanced Space that the maneuver magnitude would be anywhere from 5 to 50 cm/s.
Preliminary Results. For our first attempt at maneuver detection, we focused on an propagation window of Nov 15, 2022 to Jan 1, 2023. Within this window, we spaced initial conditions 12 hours apart, and propagated using ASSIST from the initial condition start time to the end of the propagation window. We took state measurements every 1 hour, and compared those results to the hourly Cartesian state provided by the ephemeris.
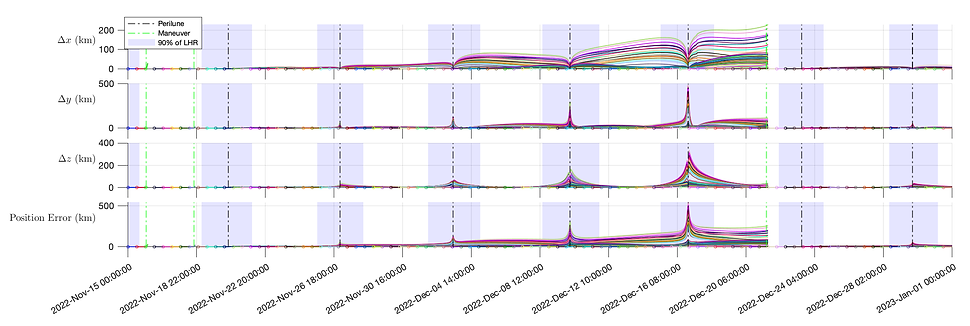
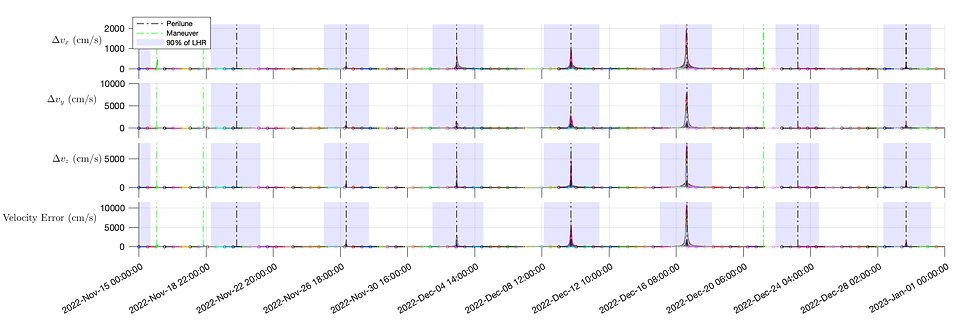
Figure 7: 12-hour spaced trajectories propagated by ASSIST from Nov 15, 2022, 00:00:00 to Jan 1, 2023, 00:00:00 TDB. Green lines indicate triggered maneuvers, black lines represent time of perilune passage, and the shaded blue areas are the regions when CAPSTONE is within 90% of the lunar Hill region.
Each marker indicates the initial condition (IC) of a new ASSIST simulation. The green lines indicate where maneuvers were detected, three total in this propagation window. When a maneuver is retrospectively detected, all propagated trajectories with ICs prior to that maneuver are cutoff at that time step. This way, the errors accumulated from the maneuver do not disrupt the rest of the propagation window. Each propagated trajectory with an IC prior to the maneuver is tested for maneuver detection, and the rate at which the trajectories trigger the maneuver of interest is tracked. The maneuver dates, as well as their trigger rates, are depicted in Table 3.
Using this metric for determining maneuvers, we made the assumption that Nov 19, 2022 00:00:00 to Dec 21, 2022 00:00:00 TDB was a large observation window where the long-range integration error analysis could be implemented. We do not claim that this window is truly free of maneuvers, as the method for maneuver detection is quite crude; rather, we assert that within this observation window, there were no triggers that would indicate a maneuver, up to our standard
Table 3: Detected CAPSTONE maneuvers from Nov. 15, 2022 to Jan. 15, 2023

3 Conclusion
In this technical report, we provide a practical framework for performing analysis on cislunar objects. We include a thorough investigation into the accuracy of open-source numerical integrators, specifically their ability to propagate the Cartesian states of objects in LPOs in the Earth-Moon system. Within this regime, we demonstrate the capabilities of ASSIST, an n-body, ephemeris-quality integrator, compared to its more notable counterpart, GMAT, an open-source system developed by NASA Goddard that supports missions in low-Earth, cislunar, and deep space. We come to the conclusion that ASSIST performs nearly as well as its GMAT counterpart, accumulating 2.41358 km/day of positional error compared to GMAT’s 2.40778 km/day. Furthermore, propagating with ASSIST is much faster than GMAT, as the regularized dynamics allow for larger time steps during close approaches. Tractably improving on the accuracy of ASSIST will require full knowledge of the orbit-determination solution used by Advanced Space.
The maneuver detection protocol used in this work is a crude, but effective, method for retrospectively detecting large trajectory correction maneuvers (TCMs) and orbital maintenance maneuvers (OMMs). The former noticeably arise in the velocity error residuals, while the latter may require a more fine-tuned method for detection. Additionally, for this work, we made the assumption that maneuvers were unlikely to occur inside the LHR due to the increase of state uncertainty there, but a more well-defined “no-go” zone is required to accurately rule out certain regions of the trajectory from containing maneuvers. Future work will center around developing a more robust framework for detecting maneuvers. One such framework that has been utilized in related research is Bayesian Online Changepoint Detection (BOCD), a method that analyzes a set of data and concurrently predicts the next unseen datum. A changepoint is detected when the actual datum does not fall within the expected distribution.
References
[1] M. Lane, “The development of an artificial satellite theory using a power-law atmospheric density representation,” in 2nd Aerospace Sciences Meeting, New York, NY, U.S.A., 1965.
[2] K. Cranford, “An improved analytical drag theory for the artificial satellite problem,” in Astrodynamics Conference, Princeton, NJ, U.S.A., 1969.
[3] D. Vallado, P. Crawford, R. Hujsak, and T. Kelso, “Revisiting spacetrack report #3,” in AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, Colorado, 2006.
[4] W. Dong and Z. Chang-yin, “An accuracy analysis of the SGP4/SDP4 model,” Chinese Astronomy and Astrophysics, vol. 34, no. 1, pp. 69–76, 2010.
[5] T. Payne, F. Hoots, A. Butkus, Z. Slatton, and D. Nguyen, “Improvements to the SGP4 propagator (SGP4-XP),” in Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, 2022.
[6] D. J. Conway and S. P. Hughes, “The General Mission Analysis Tool (GMAT): Current features and adding custom functionality,” in International Conference on Astrodynamics Tools and Techniques, Madrid, Spain, 2010.
[7] M. J. Holman, A. Akmal, D. Farnocchia, H. Rein, M. J. Payne, R. Weryk, D. Tamayo, and D. M. Hernandez, “Assist: An ephemeris-quality test particle integrator.” arXiv:2303.16246.
[8] T. Gardner, A. F. Brad Cheetham, C. Meek, E. Kayser, J. Parker, and M. Thompson, “CAPSTONE: A cubesat pathfinder for the lunar gateway ecosystem,” in Small Satellite Conference, Utah State University, Logan, UT, SSC21-II-06, 2021.
Numerical Integrator Instruction Manuals
During the process of completing my AFRL project, I found that the online documentation for the three integrators I compared, REBOUND, ASSIST, and GMAT, was slightly lacking. Thus, I developed instruction. manuals that delve into installation, usage, example problems, and a few tips and tricks that may help others avoid the issues I experienced. Attached below are the instruction manuals, as well as a .zip file containing the example code used in the manuals, the JPL ephemerides, and the SPK kernels.